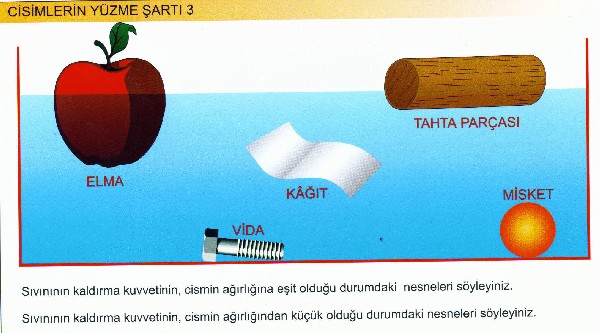
Deniz, göl ve akarsularda büyüklükleri ve cinsleri birbirinden farklı olan pek çok cisim görürüz. Bu cisimlerin kimi su yüzeyinde yüzer, kimi su içerisinde farklı derinliklere iner, kimi de dibe batar. Cisimlerin sudaki konumlarını belirleyen etkinin cevabını 2200 yıl önce Archimedes (Arşimet) vermiştir. Rivayete göre Archimedes bir gün banyo yapmak için su dolu bir küvete girer. Küvetin kenarlarından taşan suyu görünce, bu suyun ağırlığı ile kendi vücut hacminin suda kalan kısmı arasında bir ilişki olabileceğini düşünür ve cisimlerin bir sıvıda yüzmesi ya da batmasıyla ilgili bir sonuca ulaşır.
Havada uçan balonlara, uçurtmalara, kuşlara ve uçaklara olduğu gibi suda yüzen balıklara, gemilere ve kayıklara da Dünya'nın
merkezine doğru (aşağı yönde) şekildeki gibi bir çekim kuvvetinin etki eder. Dolayısıyla cismin, sıvadaki ağırlığı havadaki ağırlığından, sıvının uyguladığı kaldırma kuvveti kadar azalmış olur. Sıvı içerisine bırakılan herhangi bir cisme görüldüğü gibi değişik yönlerde ve farklı büyüklüklerde itme kuvvetleri etki eder.
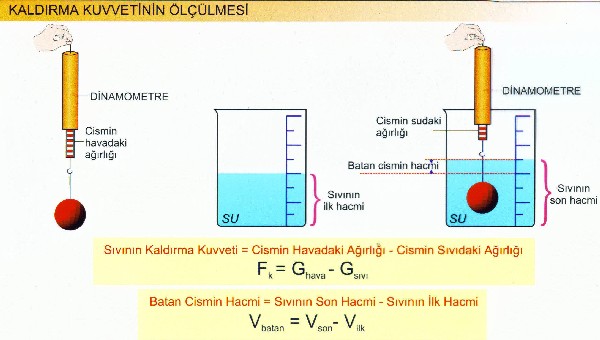
Eğer yukarıdaki deneyi etil alkol ile yapmış olsa idik Vbatan yani cismin suya girince değiştirdiği hacim miktarı , sudaki ile aynı olacaktı. Fakat kaldırma kuvveti sadece Vbatan a bağlı değildir . İçine girdiği sıvının yoğunluğuna da bağlıdır.
dsu > detil alkol suda daha fazla bir kaldırma kuvveti söz konusudur.
"Kaldırma kuvveti, cismin sıvıya batan kısmın hacmi yanında batırıldığı sıvının yoğunluğuna da bağlıdır."
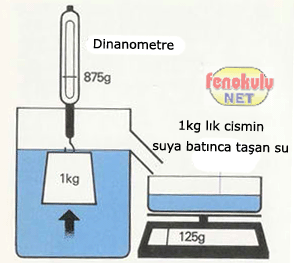
Yukarıdaki şekilde 1 kg lık cisim suya girince batan kısım kadar su taşırdı. Taşırdığı su miktarı 125 gr dır. Suyun 1 kg lık cisme uyguladığı kaldırma kuvveti siyah okun yönünde kuvvet ise 125 gr lık bir kuvvet olmuştur. Cismin ağırlığı ise 1000gr-125gr=875gr dır.
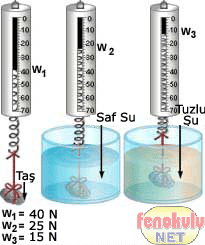
Yukarıdaki şekilde Taş havada dinamometre ile ölçülüyor ve 40 N bulunuyor.
2. Durumda suyun içine batırılarak ölçüm yapılıyor ve Dinamometredeki değer 25 N okunuyor. Buradan suyun taşa uyguladığı kuvvet 40-25=15 N olarak bulunabilir.
3. Duruda cisim tuzlu suyun içine batırılarak ölçüm yapılıyor.Dinamometredeki değer 15 N okunuyor. Buradan suyun taşa uyguladığı kuvvet 40-15=25 N olarak bulunabilir.
Buradan tuzlu suyun cisimlere daha fazla kaldırma kuvveti uyguladığı görülebilir. Tuz , suyun yoğunluğunu arttırarak kaldırma kuvvetini arttırmıştır. Denizde daha kolay yüzülmesinin sebebi suyun daha fazla kaldırma kuvveti uygulamasıdır.
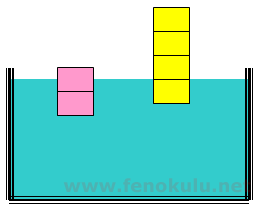
Bir sıvıya tuz katılması o sıvının yoğunluğunu arttırır. Bunun sebebi tuz moleküllerinin su molekülleri içindeki boşluklara dağılarak ağırlığını arttırdığı orandan daha az hacmini arttırmasıdır. Sıvının yoğunlunun artması sarı cisim için kaldırma kuvvetinde bir değişikliğe sebep olmaz iken pembe cisimde cisme uygulana kaldırma kuvveti artar.
Pembe Cisim İçin Sıvının Cisme Uyguladığı Kaldırma Kuvveti
Fk tuzsuz durum<Fk tuzlu durum
Ayrıca bu durum için Fk tuzlu durum= Cismin Agırlığı
Sarı Cisim İçin Sıvının Cisme Uyguladığı Kaldırma Kuvveti
Fk tuzsuz durum= Fk tuzlu durum= Cismin Agırlığı
Örnek Uygulamalar 5
http://www.fenokulu.net/kavramresim5/balon.gif
Şekildeki uçan balonu havaya bıraktığımızda balonumuzun başına neler gelir?
Atmosferde yukarı doğru çıkıldıkça açık hava basıncı azalır. Balonun içindeki basınç ile açık hava basıncı arasındaki denge Balonun içindeki basınç lehine bozulduğu için balonun hacmi artar. Belli bir yükseklikten sonra balonun plastiği bu hacim genişlemesine dayanamayarak patlar. Kafanıza gökten patlak balon düşerse hiç şaşırmayın.
Örnek Uygulamalar 6
[img] http://www.fenokulu.net/kavramresim5...rmakuvveti.gif[/img]
Şekildeki 1 numaralı kapta V hacminde sıvı vardır. Bu sıvının yoğunluğu (Özkütlesi) d dir. Bu kaba aynı sıvıdan V hacminde ilave edildiğinde sıvının son durumda ki yoğunluğu (Özkütlesi) ne olur?
Bir cismin kütlesi arttığı zaman aynı oranda hacmide artar. Bu da o cismin yoğunluğu (Özkütlesi) nu değiştirmez. Birinci durumda d=m/V ise ikinci durumda d=2m/2V dir yine bu iki değer sadeleştirmeler ile aynı değer olan d=m/V yi alır. Tüm okyanusun yoğunluğu ile bu okyanustan alınan bir damla suyun yoğunluğu aynıdır. Tonlarca ağırlığındaki bir kaya parçasının yoğunluğu ile bu kaya parçasından alınan mercimek büyüklüğündeki 2 gr katanın yoğunluğu her yerinde aynı özelliği taşıdığı taktirde aynıdır.
Örnek Uygulamalar 7
[img] http://www.fenokulu.net/kavramresim5/yogunluk.gif [/img]
Şekildeki yuvarlak cismi yandaki kapta bulunan sıvının içine attığımız taktirde bu sıvı bu cisme bir kaldırma kuvveti Fk uygular. Bu kaldırma kuvvetini nasıl hesaplayabiliriz?
[img]http://www.fenokulu.net/kavramresim5/ozkutle.gif [/img]
Bir cisme uygulanan kaldırma kuvveti Fk yer değiştiren veya taşan sıvının ağırlığına eşittir. Eğer biz yukarıdaki gibi bir sitem kurar ve taşan veya yer değiştiren sıvının ağırlığını hesaplayabilirsek kap içindeki sıvının cisme uyguladığı kaldırma kuvvetini de bulmuş oluruz.
Örnek Uygulamalar 8
[img]http://www.fenokulu.net/kavramresim5...tvehareket.gif[/img]
Şekildeki sistem dengede olduğuna göre dinamometre de okunan değer neye eşittir?
Burada 3 adet kuvvet söz konusudur. Bunlar cismin ağırlığı, sıvının kaldırma kuvveti ve dinamometrenin ölçtüğü değerdir. Cismin ağırlığı aşağı doğru, sıvının kaldırma kuvveti ve dinamometrenin ölçtüğü değer ise yukarı doğrudur. Sistem dengede olduğuna göre
Cismin ağırlığı =sıvının kaldırma kuvveti + dinamometrenin ölçtüğü değer
dinamometrenin ölçtüğü değer = Cismin ağırlığı - sıvının kaldırma kuvveti dir.
Örnek Uygulamalar 1
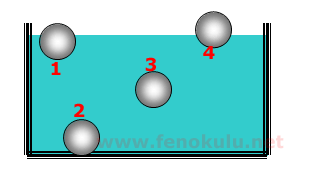
Şekildeki farklı maddelerden yapılmış, eşit hacimli 1.2.3.4. katı cisimleri şekilde ki gibi suyun içinde dengededir.
a)Suyun bu cisimlere uyguladığı kaldırma kuvvetlerini karşılaştırınız.
Fk=Cisme Uygulanan Kaldırma Kuvveti
Vb=Cismin batan kısmının Hacmi
ds=Suyun veya sıvının yoğunluğu
Fk=Vb*ds*g dir
Bu durumda g ve ds yı tüm cisimler için aynı değeri ifade ettiği için ihmal edebiliriz. Vb kısmı büyük olan cisimlerin Fk larıda büyüktür.
2. ve 3. cisimlerin su içindeki hacimleri eşit olduğu için Fk2=Fk3 dir. ve Fk1 ve Fk4 ten büyük değer alırlar.
Dolayısı ile Fk2=Fk3> Fk1> Fk4 dür.
b)Hangi cisimlerin kaldırma kuvveti ağırlığına eşit olur?
Yüzen ve askıda kalan her cismin ağırlığı kaldırma kuvvetine eşittir.
Buradan G1= Fk1 , G3= Fk3 , G4= Fk4 fakat G2>Fk2 dir.
c)Cisimleri yoğunluklarına göre nasıl sıralarız?
Cisimler yoğunluklarına göre sıralarken az yoğun olanın sürekli çok yoğun olanın üstüne çıktığını bilmek gereklidir. Buradan hareketle d2>d3>d1>d4 diyebiliriz.
Örnek Uygulamalar 2
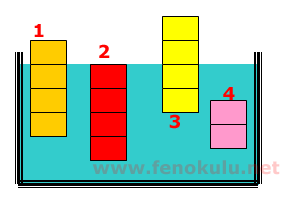
Eşit bölmeli şekildeki 1,2,3,4 numaralı cisimler dengededir.
a)Hangi cisimlere etkiyen kaldırma kuvvetleri eşittir?
Burada yine Fk=Vb*ds*g dir
Bu durumda g ve ds yı tüm cisimler için aynı değeri ifade ettiği için ihmal edebiliriz. Vb kısmı büyük olan cisimlerin Fk larıda büyüktür.
1. cisim Fk1=3V
2. cisim Fk2=4V
3. cisim Fk3=2V
4. cisim Fk4=2V dir dolayısı ile Fk3= Fk4 diyebiliriz.
b)Çözeltiye tuz katılırsa cisimlere uygulanan kaldırma kuvveti nasıl değişir?
Hiçbirinin kaldırma Kuvveti değişmez çünkü tuz katınca suyun yoğunluğu artar. Fakat aynı oranda cisimlerin suya batan kısımlarının hacimleri azalır. Buda Fk=Vb*ds*g dir eşitliğinde bir değişime sebep olmaz. Dolayısı ile yine her cisme uygulanan kaldırma kuvveti tuz katılmadan önceki değeri alır ve değişmez iken suya bata kısımların hacimleri azalıp suyun yoğunluğu artar.
Örnek Uygulamalar 3
Aşağıdaki şekilde havası boşaltılmış fanusta farklı hacimlerdeki iki cisim şekildeki gibi dengededir. Şekildeki havası boşaltılmış fanusa hava verildiğinde son durum ne olur?
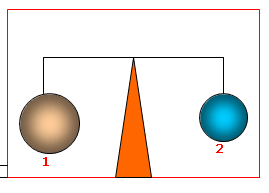
Havasız ortamda sistemin dengede kalması 1. ve 2. cisimlerin ağırlıklarının eşit olduğu anl***** gelir. Fanusa hava verildiğinde hava 1. ve 2. cisimlere kaldırma kuvveti uygular. Hava tarafından hacmi büyük olan 1. cisme daha fazla kaldırma kuvveti uygulanır.. Bunun sebebi aynı kütleye sahip olan iki cisimden 1. sinin hacminin büyük olması nedeni ile daha düşük yoğunluğa sahip olmasıdır. Dolayısı ile Fanusa hava verildiğinde sistem aşağıdaki şekli alır.
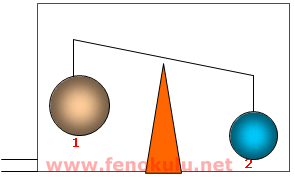
Örnek Uygulamalar 4

Bir sıvıya tuz katılması o sıvının yoğunluğunu arttırır. Bunun sebebi tuz moleküllerinin su molekülleri içindeki boşluklara dağılarak ağırlığını arttırdığı orandan daha az hacmini arttırmasıdır. Sıvının yoğunlunun artması sarı cisim için kaldırma kuvvetinde bir değişikliğe sebep olmaz iken pembe cisimde cisme uygulana kaldırma kuvveti artar.
Pembe Cisim İçin Sıvının Cisme Uyguladığı Kaldırma Kuvveti
Fk tuzsuz durum<Fk tuzlu durum
Ayrıca bu durum için Fk tuzlu durum= Cismin Agırlığı
Sarı Cisim İçin Sıvının Cisme Uyguladığı Kaldırma Kuvveti
Fk tuzsuz durum= Fk tuzlu durum= Cismin Agırlığı
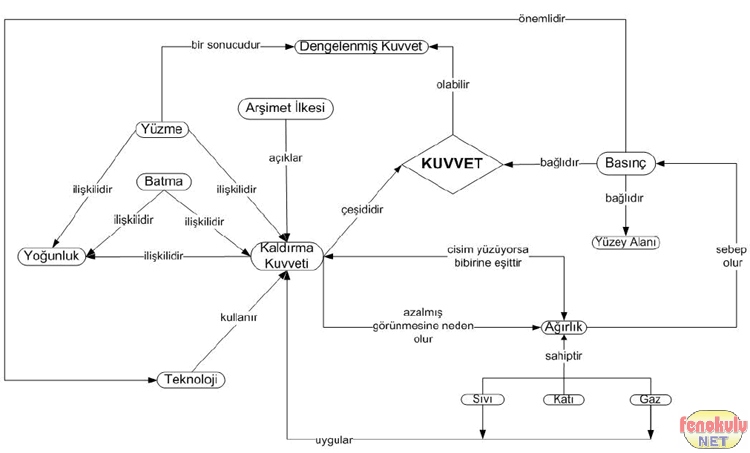
Basınç Sıvı İlişkisi
Hangi amaçla olursa olsun su sıkıştırılamaz. Bu yüzden su yüzeyine dışardan uygulanan bir basınç suyun içinde her yöne doğru eşit olarak nakledilir. Bu işlem hidrolik kaldırma prensibi veya Pascal prensibi olarak bilinir. Vücut dokularının hepsinin büyük kısmı sudan ibaret olduğu için dalgıca uygulanan basınç bütün dokulara doğrudan doğruya ve eşit olarak tüm doğrultularda dağılır. Bu basınç hiç bir zaman vücudumuzdaki tek bir noktayı direk olarak etkilemez. Sıvılar sıkıştırılamaması insan vücudunun çok büyük derinliklerde dahi basınca dayanıklı olmasını sağlar. Vücudumuzda çeşitli hava boşlukları vardır. Derinlere inildikçe duyulan rahatsızlık, suyun bu hava boşluklarına yapmış olduğu basınçtan dolayıdır. Aşağıya doğru inildikçe artan su miktarı ile basınç da artar. Bu artış her 1 metrede 76mmHg’dir. Tatlı su daha az yoğun olduğu için bu basınç artışı daha azdır. Bu değerler sabittir, derinlik artışından etkilenmezler.
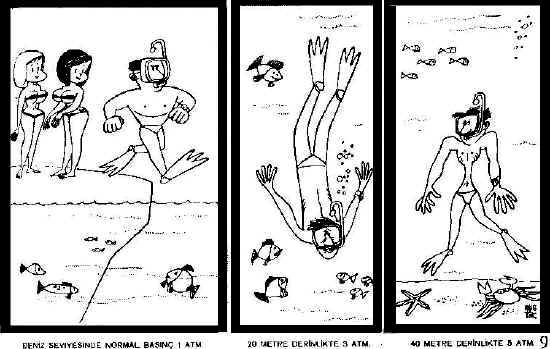
Suyun altında tek basınç kaynağı suyun uyguladığı basınç değildir. Buna ek olarak, su yüzeyine atmosferin uyguladığı basınç da vardır. Bu yüzden herhangi bir derinlikteki basınç, 0 derinlikteki suyun uyguladığı basınç ile su yüzeyine uygulanan atmosfer basıncının toplanması ile bulunur. Örneğin; 30 metrede bize uygulanan basınç ne olur?
30 metrede suyun oluşturduğu basınç 3 atmosferdir.Buna yüzeydeki 1 atmosfer basıncı eklersek 4 atmosfer buluruz
Yüzerlilik
Yüzerlilik cisimlerin yüzmesine sebep olan güç veya sıvı içindeki herhangi bir nesnenin yukarıya doğru yükselmesini sağlamak için sarf edilen güç olarak açıklanır. Yunan matematikçi Archimedes bu olayın ana prensiplerini açıklayan ilk kişidir. Bu prensibe göre tamamen yada kısmen su içine batmış herhangi bir cismi yüzdürmek için gereken güç o cismin taşırdığı suyun ağırlığına eşittir. Arşimet’in prensibi tüm sıvılar içindeki tüm maddeler için doğrudur. Buna rağmen maddenin yüzerliliğindeki değişme içine battığı sıvının yoğunluğuna bağlıdır. Çok yoğun bir sıvı daha yoğun bir kaldırma kuvveti sağlayacaktır. 1cm3 saf suyun ağırlığı 1.0 gr.dır. İngiliz sistemine göre ise 62.4 pound/foot3 olarak ifade edilir. Diğer bir yandan deniz suyunun içinde tuz çözünmüş halde bulunduğundan dolayı deniz suyu tatlı sudan daha yoğundur. İçerdiği tuza bağlı olaraktan deniz suyunun ağırlığı 64 pound./foot3 (1 .O2gr). Ayrıca ağırlığının ve yoğunluğunun fazla olmasından dolayı, deniz suyu batmış maddelere daha çok kaldırma kuvveti sağlayabilir. Böylece tatlı ve tuzlu sularda dalış yapan dalgıçların neden farklı yüzerliliklere sahip oldukları açıklanmış olur. Tuzlu suda yüzerliliğin fazla olmasının nedeni su yoğunluğunun fazla olmasıdır.
Özgül ağırlık bir birim katı yada sıvının yoğunluğunun saf suyun yoğunluğuna oranıdır. Özgül ağırlığı 1.0'dan daha az olarak tanımlanan maddeler sudan daha hafif yoğunluğa sahiptir ve suda yüzecekler demektir. Özgül ağırlıkları 1 .O’dan büyük olan maddelerim yoğunlukları sudan fazladır ve suda batacaklar demektir. Yüzerlilik olayında insanlar iki şekilde sınıflandırılabilir. su üstünde kalanlar ve batanlar. Bu yüzerlilik karakteristikleri vücudumuzdaki çeşitli dokuların kendilerine has özelliklerine bağlıdır. Çünkü her doku farklı özgül ağırlığa sahiptir. Öreğin yağ dokusu 0.7-0.9 arasında kas dokusu 1.08, kemik dokusu 1.9 özgül ağırlığa sahiptir. İnsan vücudunun özgül ağırlığı yaklaşık olarak 1 .0’dır. Yani bunun anlamı insan vücudu ya su üstünde kalmak, yada pek az olarak su içine batırıldığında batmak eğilimindedir. Fakat dalgıç dalış malzemesini kuşandığında vücut ağırlığının üzerine yeni ağırlık eklenmiş olur. Bununla birlikte bu fazladan ağırlık oldukça fazla su taşıracaktır. Su taşırmadaki artışın bu net etkisi dalgıcın yüzerliliğinde genellikle yüksek bir artışla sonuçlanır. Çeşitli yüzerlilik olaylarının daha kolay açıklanması için; pozitif, negatif, nötr terimleri kullanılmıştır. Nesne, su üzerinde kalabiliyorsa pozitif yüzerlilikle, batıyorsa negatif yüzerlilikli denir. Eğer, nesne durma eğiliminde ise yani ne batıyor ne de yüzüyorsa nötr yüzerlilikli tanımı kullanılır. Bu üç yüzerlilik durumunu dalgıçlar iyi bir şekilde uygulamalıdır. Çünkü bu durumlar su üstünde kalmak veya batmak niyetinde olan dalgıcın bunu yapabilmesi için harcadığı enerjiyi en aza indirmesini sağlar.
Eğer dalgıç yüzerlilik kavramını iyi anlarsa bu bilgilerini dalışta karşılaştığı problemlerde pratik olarak uygulayabilir. Varsayalım bir dalgıç suya düşmüş, pahalı ve büyük dıştan takılan bir motorun yüzeye çıkarılması problemi ile karşılaşsın. Karada motorun ağırlığı 75 kg. ise suyun uyguladığı kaldırma kuvvetinin dışında uygulanması gereken kaldırma kuvveti ne kadar olmalıdır ki motorun zeminden kaldırılması sağlanabilsin? İlk önce dalgıç, motorun taşıracağı suyun hacmini hesaplamalıdır. Taşan su hacminin ağırlığı makineyi yukarı kaldırmak için sarf edilmesi gereken kaldırma kuvvetine eşit olacaktır. Bu örnekte motorun 33 lt su taşırdığı kabul edilmiştir. Bundan dolayı motoru yukarı kaldırmak için su tarafından uygulanan kaldırma kuvveti 33 kg’dir. Fakat motorun ağırlığı ise 75 kg’dir. Şimdi problemi, zıt kuvvetleri karşılaştırmak için inceleyelebiliriz. Motoru aşağıya çeken 75 kg’lik yer çekimi ve karşısında yukarı kaldırmaya çalışan 33 kg’lik kaldırma kuvveti var. Motorun nötr yüzerliliğini sağlamak için 42 kg’lik kaldırma kuvveti sağlanmalıdır. 1 lt deniz suyunun ağırlığı yaklaşık olarak 1 kg. gelmektedir. Bu yüzden 42 kg.’lik bir kaldırma kuvveti, 421t suyun boşaltılmasına eşit olacaktır.
Eğer bu motoru kaldırmak için 100lt’lik bir balon kullanılacaksa bu balonun 3/7’sinin hava ile doldurulması motoru nötr yüzerliliğe kavuşturacaktır.
Cisimlerin Yüzme Şartı ve kaldırma kuvveti
Cisimler nasıl yüzerler?
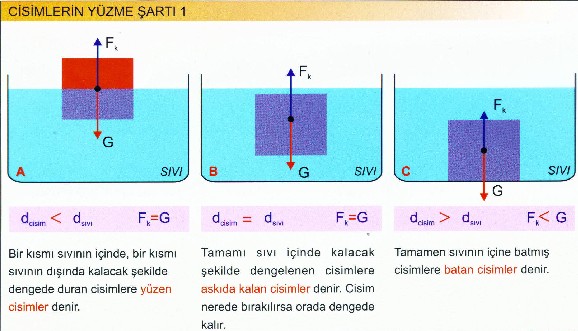
Yüzme şartı

Sıvıların kaldırma kuvvetini nasıl ölçeriz?
Kaldırma kuvvetinin ölçülmesi

Sıvı içinde dengede olan cisme uygulanan kaldırma kuvvetinin değerini neler değiştirir?
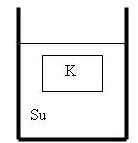
Aşağıdaki işlemlerden hangisinin yapılması su içinde şekildeki gibi
Dengede olan K cismine uygulanan kaldırma kuvvetinin değerini değiştirir?
I. Kaptaki suya tuz döküp karıştırmak
II. Kaptaki suyun bir kısmını boşaltmak
III. Cismin yarısını kopartarak suya bırakmak
IV. Kabı deniz seviyesinden yukarılara çıkarmak
A. I ve II
B. II, III ve IV
C. III ve IV
D. I, II ve III
I-Tuz yoğunluğu artırır ama cismin batan kısmının hacmi de o oranda azalacağı için DEĞİŞTİRMEZ
II- Kaptan boşaltılan su miktarının ne kadar olduğu mutlaka belirtilmeli.Cisim askıda kalacak kadar
Boşaltılırsa kaldırma kuvveti DEĞİŞTİRMEZ.
Cisim batacak şekilde boşaltılırsa DEĞİŞTİRİRİR.
III-Cismin yarısını koparırsan taşırdığı su miktarı azalacağı için hem cismin ağırlığı hem de ayni oranda
kaldırma kuvveti azalır.Yani DEĞİŞTİRİR.
IV-Kabı deniz seviyesinden yukarı çıkarırsan cismin ağırlığı azalır ,hacmi sabit kaldığına göre cismin
özgül ağırlığı da azalır.Cisim yukarı çıkarak batan kısmin hacmi de azalacağı için kaldırma kuvveti de
azalır.Zaten yüzen ve askıda kalan cismin ağırlığı azaldığında kaldırma kuvveti de ayni oranda
azalır. Fk=G den DEĞİŞTİRİR
Cisimler nasıl yüzerler?

Yüzme şartı

Sıvıların kaldırma kuvvetini nasıl ölçeriz?
Kaldırma kuvvetinin ölçülmesi

Sıvı içinde dengede olan cisme uygulanan kaldırma kuvvetinin değerini neler değiştirir?
Aşağıdaki işlemlerden hangisinin yapılması su içinde şekildeki gibi
Dengede olan K cismine uygulanan kaldırma kuvvetinin değerini değiştirir?
I. Kaptaki suya tuz döküp karıştırmak
II. Kaptaki suyun bir kısmını boşaltmak
III. Cismin yarısını kopartarak suya bırakmak
IV. Kabı deniz seviyesinden yukarılara çıkarmak
A. I ve II
B. II, III ve IV
C. III ve IV
D. I, II ve III
I-Tuz yoğunluğu artırır ama cismin batan kısmının hacmi de o oranda azalacağı için DEĞİŞTİRMEZ
II- Kaptan boşaltılan su miktarının ne kadar olduğu mutlaka belirtilmeli.Cisim askıda kalacak kadar
Boşaltılırsa kaldırma kuvveti DEĞİŞTİRMEZ.
Cisim batacak şekilde boşaltılırsa DEĞİŞTİRİRİR.
III-Cismin yarısını koparırsan taşırdığı su miktarı azalacağı için hem cismin ağırlığı hem de ayni oranda
kaldırma kuvveti azalır.Yani DEĞİŞTİRİR.
IV-Kabı deniz seviyesinden yukarı çıkarırsan cismin ağırlığı azalır ,hacmi sabit kaldığına göre cismin
özgül ağırlığı da azalır.Cisim yukarı çıkarak batan kısmin hacmi de azalacağı için kaldırma kuvveti de
azalır.Zaten yüzen ve askıda kalan cismin ağırlığı azaldığında kaldırma kuvveti de ayni oranda
azalır. Fk=G den DEĞİŞTİRİR
Bazı Cisimler Neden Yüzer veya Batar? (Konu Anlatımı)

Bir cismin eşit kollu terazi ile kütlesini , şekli düzgün değilse dereceli silindir ile hacmini ölçeriz. Eğer cisim düzgün hacimli bir cisim ise matematiksel bağlantılar ile hacmini bulabiliriz.
Yoğunluğu yukarıdaki gibi hesaplayabiliriz.
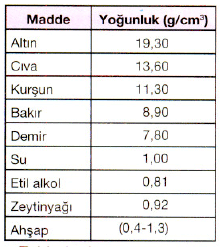
Yukarıda bazı maddelerin yoğunluk değerleri gözükmektedir.
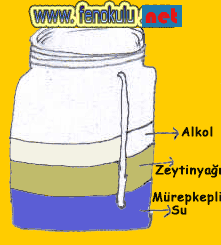
Yukarıda Yoğunluğu farklı ve birbirine karışmayan sıvıların bir kabın içinde sıralanışlarını görüyorsunuz.
Yoğunluğu en az olan her zaman üstte bulunur.

Kaldırma kuvvetinin, yeri değişen sıvının ağırlığı kadar olduğunu biliyoruz. Bu yüzden cismin suya batan hacmi arttıkça, dinamometrenin gösterdiği ağırlık değeri azalır. Cisim suda yüzmeye başladığı anda ise dinamometre sıfırı gösterir. Bu sırada cisme etki eden kaldırma kuvveti cismin ağırlığına eşit olur. Aynı şekilde, kaseye taşan sıvı ağırlığı da cismin havadaki ağırlığına eşit olur.

Şekildeki gemiye uygulanan kaldırma kuvvetinin etki alanı sadece batan kısmının alanına veya başka bir değişle batan kısmının hacmi ile ilişkilidir.
Suyun Yoğunluğu > Gemini Yoğunluğunudur
Gemini Yoğunluğunu = Geminin Kütlesi /Geminin Suya Batan Kısmının Hacmi ile bulabiliriz.

Bir cismin eşit kollu terazi ile kütlesini , şekli düzgün değilse dereceli silindir ile hacmini ölçeriz. Eğer cisim düzgün hacimli bir cisim ise matematiksel bağlantılar ile hacmini bulabiliriz.
Yoğunluğu yukarıdaki gibi hesaplayabiliriz.

Yukarıda bazı maddelerin yoğunluk değerleri gözükmektedir.

Yukarıda Yoğunluğu farklı ve birbirine karışmayan sıvıların bir kabın içinde sıralanışlarını görüyorsunuz.
Yoğunluğu en az olan her zaman üstte bulunur.

Kaldırma kuvvetinin, yeri değişen sıvının ağırlığı kadar olduğunu biliyoruz. Bu yüzden cismin suya batan hacmi arttıkça, dinamometrenin gösterdiği ağırlık değeri azalır. Cisim suda yüzmeye başladığı anda ise dinamometre sıfırı gösterir. Bu sırada cisme etki eden kaldırma kuvveti cismin ağırlığına eşit olur. Aynı şekilde, kaseye taşan sıvı ağırlığı da cismin havadaki ağırlığına eşit olur.

Şekildeki gemiye uygulanan kaldırma kuvvetinin etki alanı sadece batan kısmının alanına veya başka bir değişle batan kısmının hacmi ile ilişkilidir.
Suyun Yoğunluğu > Gemini Yoğunluğunudur
Gemini Yoğunluğunu = Geminin Kütlesi /Geminin Suya Batan Kısmının Hacmi ile bulabiliriz.
Tekneler Nasıl Yüzer?
Bir tekne suya indirildiğinde suyu yanlara iter yani suyun yerini değiştirir. Su da buna kaldırma kuvveti ile cevap verir. Kaldırma kuvvetinin büyüklüğü, yeri değiştirilen suyun ağırlığına bağlıdır. Bir cismin yüzebilmesi için, yerini değiştirdiği suyun kaldırma kuvvetinin en azından cismin ağırlığına eşit olması gerekir. Bir cismin yerini değiştirdiği suyun miktarı, o cismin biçimine bağlıdır. Örneğin çamurdan yapılmış bir top batar, ama eğer bu topa içi boş bir kase biçimi verirseniz yüzer. Çamurun biçimini değiştirerek onun terini değiştirdiği su miktarını artırmış olursunuz. Tekne yapımcılarının yaptığı da işte budur. Çelik bir levha batar ama çelikten yapılmış bir gemi yüzer


Bir tekne suya indirildiğinde suyu yanlara iter yani suyun yerini değiştirir. Su da buna kaldırma kuvveti ile cevap verir. Kaldırma kuvvetinin büyüklüğü, yeri değiştirilen suyun ağırlığına bağlıdır. Bir cismin yüzebilmesi için, yerini değiştirdiği suyun kaldırma kuvvetinin en azından cismin ağırlığına eşit olması gerekir. Bir cismin yerini değiştirdiği suyun miktarı, o cismin biçimine bağlıdır. Örneğin çamurdan yapılmış bir top batar, ama eğer bu topa içi boş bir kase biçimi verirseniz yüzer. Çamurun biçimini değiştirerek onun terini değiştirdiği su miktarını artırmış olursunuz. Tekne yapımcılarının yaptığı da işte budur. Çelik bir levha batar ama çelikten yapılmış bir gemi yüzer


Gazlar da Cisimlere Kaldırma Kuvveti Uygular mı? (Konu Anlatımı)
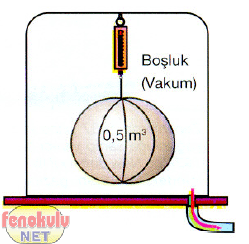
Normal bir ortamda bir tenis topunun ağırlığını dinamometre ile ölçelim. Daha sonra bu sistemi şekildeki gibi ortamdaki havayı pompa ile alabileceğimiz vakumlu bir sisteme koyup içerideki havayı alalım. Dinamometrede, havayı aldıktan sonra gözlemlediğimiz değer daha da artacaktır. Çünkü ortamdan havayı kaldırarak havanın topa uygulamış olduğu kaldırma kuvvetini de kaldırdık. Buda sonraki değerin artmasına sebep oldu.
Eğer havanın kaldırma kuvveti cismin ağırlığından büyük ise o cisim uçar. Uçan balonlar ve zeplinler bu mantık ile havada uçar veya yükselir.
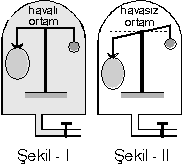
Şekil – I de hava ortamında eşit kollu terazinin kollarına asılarak hacimleri farklı cisimler dengeleniyor. Hava boşaltıldığında terazi Şekil – II deki durumu alıyor. Çünkü hava ortamında, hacmi büyük olan cisme daha fazla kaldırma kuvveti uygulanır. Hava dışarı alındığında bu kuvvet ortadan kalktığı için hacmi büyük olan cisim aşağı iner.
Eğer havasız ortamda aynı terazi dengelendikten sonra hava ort***** çıkarılsaydı, bu durumda da hacmi büyük olan cisim yukarı kalkardı.
Cisim ne kadar büyürse ona etki eden havanın kaldırma kuvveti fazlalaşır. Bu yüzden 0,1 m3 cisme yaklaşık 1 N' luk kaldırma kuvveti etki ederken 0,5 m3' lük cisme yaklaşık 5 N' luk kaldırma kuvveti etki eder.

Balon, hava akışkanlar içerisine konulmuş bir cisimdir. Gaz sızdırmaz ipekli veya pamuklu kumaştan ya da plastik maddelerden yapılan balonun havada uçabilmesi için ortalama yoğunluğunun havanın yoğunluğundan az olması gerekir.
Bunun için:
. Balon içerisindeki hava ısıtılabilir.
. Balon içerisine havadan daha hafif olan helyum veya hidrojen gibi başka bir gaz doldurulabilir.
Her iki durumda da balon havada yükselir.
Bir uçan balonun irtifasının (yerden yüksekliğinin) kontrolü, balon ve içindeki gazdan oluşan sistemin yoğunluğunun değiştirilmesi ile sağlanır. Yani sistemin yoğunluğu azaltılırsa balon irtifa kazanır yükselir , tersi yapılırsa irtifa kaybeder yere yaklaşır.
Bir cismin kendinden daha yoğun cisimler içinde yüzer veya uçar.
Atmosferde yukarılara doğru çıktıkça gazların (atmosferin) yoğunluğu azalır. Bu sebeple balonların uzaya kadar çıkmaları çok zordur. Bir yükseklikten sonra balonun atmosferden az olan yoğunluğu belli bir yükseklikten sonra eşitlenebilir. Yalnız şunu da unutmamak gerekir. Yukarılara doğru çıktıkça yoğunlukla beraber atmosferin basıncıda azalır.

Normal bir ortamda bir tenis topunun ağırlığını dinamometre ile ölçelim. Daha sonra bu sistemi şekildeki gibi ortamdaki havayı pompa ile alabileceğimiz vakumlu bir sisteme koyup içerideki havayı alalım. Dinamometrede, havayı aldıktan sonra gözlemlediğimiz değer daha da artacaktır. Çünkü ortamdan havayı kaldırarak havanın topa uygulamış olduğu kaldırma kuvvetini de kaldırdık. Buda sonraki değerin artmasına sebep oldu.
Eğer havanın kaldırma kuvveti cismin ağırlığından büyük ise o cisim uçar. Uçan balonlar ve zeplinler bu mantık ile havada uçar veya yükselir.

Şekil – I de hava ortamında eşit kollu terazinin kollarına asılarak hacimleri farklı cisimler dengeleniyor. Hava boşaltıldığında terazi Şekil – II deki durumu alıyor. Çünkü hava ortamında, hacmi büyük olan cisme daha fazla kaldırma kuvveti uygulanır. Hava dışarı alındığında bu kuvvet ortadan kalktığı için hacmi büyük olan cisim aşağı iner.
Eğer havasız ortamda aynı terazi dengelendikten sonra hava ort***** çıkarılsaydı, bu durumda da hacmi büyük olan cisim yukarı kalkardı.
Cisim ne kadar büyürse ona etki eden havanın kaldırma kuvveti fazlalaşır. Bu yüzden 0,1 m3 cisme yaklaşık 1 N' luk kaldırma kuvveti etki ederken 0,5 m3' lük cisme yaklaşık 5 N' luk kaldırma kuvveti etki eder.

Balon, hava akışkanlar içerisine konulmuş bir cisimdir. Gaz sızdırmaz ipekli veya pamuklu kumaştan ya da plastik maddelerden yapılan balonun havada uçabilmesi için ortalama yoğunluğunun havanın yoğunluğundan az olması gerekir.
Bunun için:
. Balon içerisindeki hava ısıtılabilir.
. Balon içerisine havadan daha hafif olan helyum veya hidrojen gibi başka bir gaz doldurulabilir.
Her iki durumda da balon havada yükselir.
Bir uçan balonun irtifasının (yerden yüksekliğinin) kontrolü, balon ve içindeki gazdan oluşan sistemin yoğunluğunun değiştirilmesi ile sağlanır. Yani sistemin yoğunluğu azaltılırsa balon irtifa kazanır yükselir , tersi yapılırsa irtifa kaybeder yere yaklaşır.
Bir cismin kendinden daha yoğun cisimler içinde yüzer veya uçar.
Atmosferde yukarılara doğru çıktıkça gazların (atmosferin) yoğunluğu azalır. Bu sebeple balonların uzaya kadar çıkmaları çok zordur. Bir yükseklikten sonra balonun atmosferden az olan yoğunluğu belli bir yükseklikten sonra eşitlenebilir. Yalnız şunu da unutmamak gerekir. Yukarılara doğru çıktıkça yoğunlukla beraber atmosferin basıncıda azalır.
|
|